Variance in Terms of Conditional Variance
Try not to confuse properties of expected values with properties of. Let X and Y be marginally standard Normal random variables with CovXY ˆ.

L13 6 The Conditional Variance Youtube
E X k Y R x k f X Y x Y d x R f X Y x Y d x.

. Markov chain Monte Carlo MCMC simulation and prediction schemes are. The conditional variance-covariance matrix of Y given that X x is equal to the variance-covariance matrix for Y minus the term that involves the covariances between X and Y and the variance-covariance matrix for X. Granting of variance will be generally consistent with the purposes goals objectives and policies of the comprehensive plan and the code and will not adversely effect adjacent land.
Similar to the conditional expectation we can define the conditional variance of X VarXYy which is the variance of. The square root of the variance of a random variable is called itsstandard deviation. In the linear regression of ξ2 on ξ1 the mean conditional variance is.
Many distributions the simplest measure to calculate is the variance or more precisely the square root of the variance. Granting of variance is the minimum variance that will make possible the reasonable use of the parcel of land building or structure and. 76 E D ξ 2 x 1 D ξ 2 1 ρ 2.
Since you say that you have the joint probability measure function to evaluate you shall be able to calculate the conditional variance of X under Y. Variance of the Conditional Expected Value. Using the second formula for variance we have VarEYX EEYX2 - EEYX2 Since EEYX EY this gives VarEYX EEYX2 - EY2.
If I was to conclude a statement is it acceptable to stay the model captures volatility clustering via 2 period lags. Beta_0 is just a constant so it drops out as does beta_1 later in the calculations. For now we will call this conditional variance-covariance matrix A as shown below.
A Distinguish between the terms conditional variance and unconditional variance. Investors use variance to see how much risk an investment carries and whether it will be profitable. The Variance The conditional variance of the average treatment effect estimator depends on the conditional variance of the outcome differences gx.
One-step-ahead volatility forecasts ii. And similarly in the discrete case. If X has high variance we can observe values of X a long way from the mean.
2 The conditional use or variance is the minimum that will make possible the reasonable use of land building or structure. However since we know that the variance is time varying we also know that sigma_t2 has a time dependent structure and exhibits autocorrelations so do the squares returns residuals. For now we will call this conditional variance-covariance matrix A as shown below.
The variance of a random variable X with expected value EX is de ned as varX E X 2. The variance is the mean squared deviation of a random variable from its own mean. We have already seen that the conditional law of Y given X x is Nˆx1 ˆ2.
Conditional variances are also random variables dependent on condition which may characterized by the mean values and variances. B If u follows a GARCH 11 process what would be the likely result if a regression of the form. The conditional variance-covariance matrix of Y given that X x is equal to the variance-covariance matrix for Y minus the term that involves the covariances between X and Y and the variance-covariance matrix for X.
Note that the conditional variance of epsilon_t is equal to sigma_t2. Which of the two is more likely to be relevant for producing i. And the variance of conditional mean value is.
For what comes next we will need to consider the variance of the conditional expected value. Using the second formula for variance we have VarEYX EEYX2 - EEYX2 Since EEYX EY this gives VarEYX EEYX2 - EY2. V a r X Y E X 2 Y E X Y 2 E X E X Y 2 Y In the continuous case for k N.
Variance is a measurement of the spread between numbers in a data set. As with expectations variances and covariances can also be calculated conditionally on various pieces of information. For what comes next we will need to consider the variance of the conditional expected value.
I am also not sure if I should state some stability conditions in this question similar to AR1 processes eg alpha_1 1 and alpha_2 1 since these are variances do those conditions apply. In probability theory the law of total variance or variance decomposition formula or conditional variance formulas or law of iterated variances also known as Eves law states that if X displaystyle X and Y displaystyle Y are random variables on the same probability space and the variance of Y displaystyle Y is finite then Var E Var. Section three introduces the conditional mean and conditional variance model along with parameter estimation used in this work fitting of the model is discussed in section four.
Variance of the Conditional Expected Value. Estimating these con sistently requires non-parametric estimation of conditional expectations which in turn requires choices of smoothing parameters that depend on sample size see. Which coincides with the law of cases for expectation.
I believe this all works because since we provided that baru and hatbeta_1 - beta_1 are uncorrelated the covariance between them is zero so the variance of the sum is the sum of the variance. The variance measures how far the values of X are from their mean on average. Variance is also used to.
To define conditional variance VarY jX X where x VarY jX x we need EjYj. We can model it using GARCH class of models which can very roughly be seen as ARMA models for. 3 The granting of the conditional use or variance will be in harmony with the general purpose and intent of GCC Titles 22 23 and 24 and other applicable provisions of the Grant County Code.
Let X be any random variable. The square root of the variance of a random variable is called its standard deviation sometimes denoted by sdX. The variance of X is VarX E X µ X 2 EX EX.
77 D E ξ 2 x 1 D ξ 2 ρ 2.
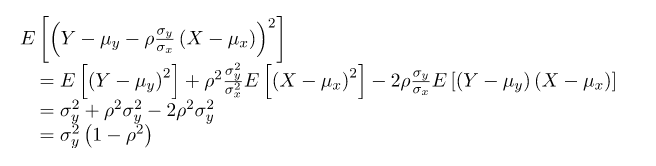
Conditional Variance And Predictions Its Important Properties With 5 Example Lambda Geeks

L13 7 Derivation Of The Law Of Total Variance Youtube

Conditional Variance And Predictions Its Important Properties With 5 Example Lambda Geeks

Solved 4 Analogous To Conditional Expectation The Chegg Com

5 1 Two Discrete Random Variables Example Two Discrete Random Variables Figure 5 1 Joint Probability Distribution Of X And Y In Example Ppt Download

Statistics Conditional Variance Mathematics Stack Exchange

L13 6 The Conditional Variance Youtube

Statistics Conditional Variance For Discrete Continous Random Variable X Mathematics Stack Exchange

Probability Variance Of Expected Value Is The Formula Right Cross Validated
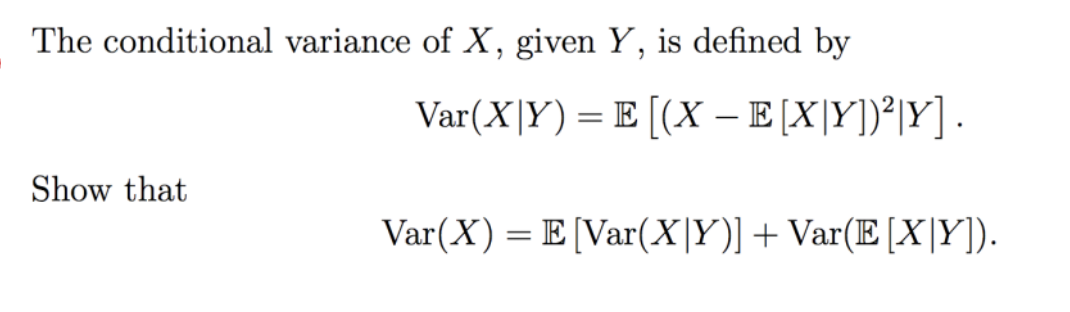
Solved The Conditional Variance Of X Given Y Is Defined Chegg Com
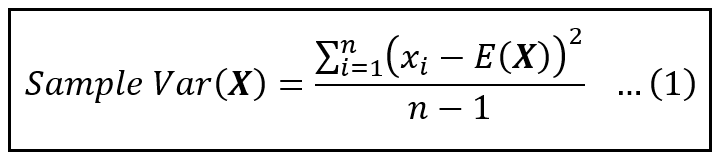






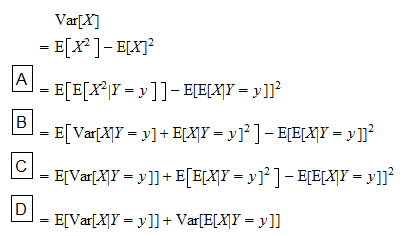
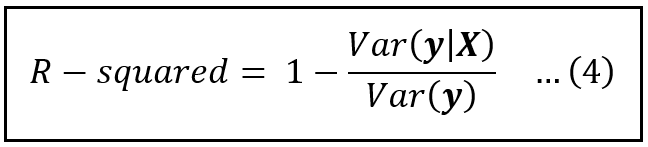
Comments
Post a Comment